목차
병합 정렬(Merge Sort)
병합 정렬은 O(n log n) 속도를 가진 효율적인 정렬 알고리즘입니다. O(n log n)을 좀 더 자세히 알아보자면 , O(n log n)은 O(n) x O(log n)과 같습니다.
병합 정렬 하나의 큰 문제를 두 개의 작은 문제로 나눈 후 각자 계산 후 합치게 됩니다. 즉 반으로 정확히 나누고 나중에 정렬하는 게 핵심입니다.
개념
1. 카드를 병합 정렬해보겠습니다 아래 그림과 같이 정렬되지 않은 카드를 받았다고 가정해봅시다.
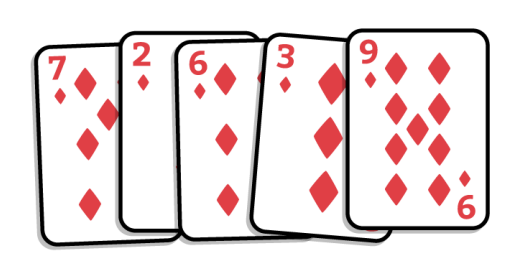
2. 병합 정렬 특징상 먼저 카드를 반으로 나눕니다. 이제 두 개의 정렬되지 않은 카드 뭉치가 됩니다.
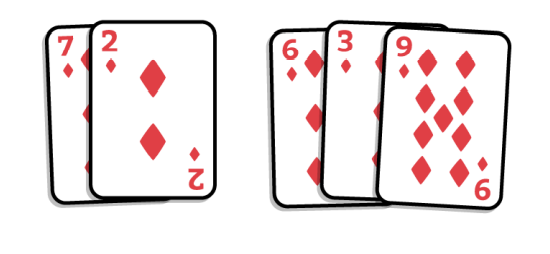
3. 그리고 나눌 수 없을 때까지 나눠서 1배 열인 상태로 시작합니다.

4. 이제 나눴던 역순으로 다시 합칩니다. 합치는 순간 정렬이 실행됩니다.

5. 이렇게 모두 병합될 때까지 반복하면 정렬되게 됩니다.
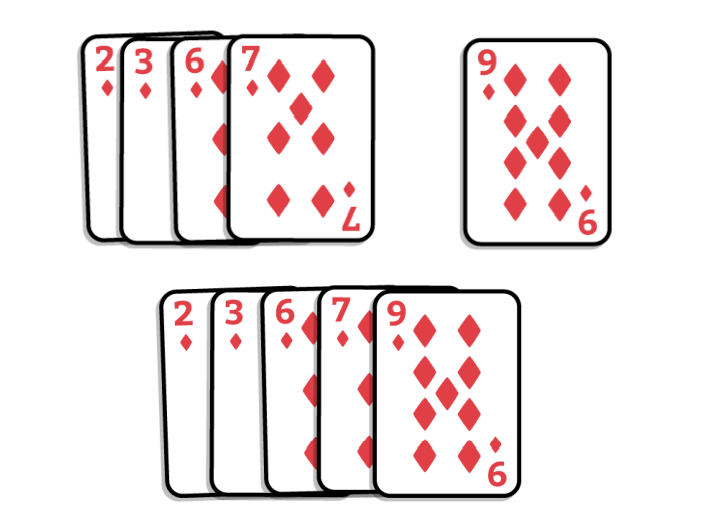
병합 정렬 구현
위에서 설명했듯이 병합 정렬은 리스트에 있는 element들을 나눌수없을때까지 나누고 합쳐가며 정렬되는 구조입니다. 그러므로 병합정렬에 필요한 함수는 나누는 함수(split), 합치는 함수(merge) 압니다.
나누기 함수 구현(Split)
2개 미만의 리스트는 정렬됐다고 정의합니다. 병합 정렬은 이 특성을 이용하여 더 이상 나눌 수 없을 때까지 즉 리스트당 element가 하나만 남을 때까지 나눕니다.
먼저 나누는 함수를 만들어보겠습니다.
Split
fun <T:Comparable<T>> List<T>.mergeSort(): List<T>{
//1
if(this.size < 2) return this
val middle = this.size / 2
//2
val left = this.subList( 0, middle ).mergeSort()
val right = this.subList( middle, this.size ).mergeSort()
// ...still more to come
}코드를 설명해 보겠습니다.
1. 일단 반복문에서는 반복문을 끝낼 기준인 기본값이 필요합니다. 이 반복문은 size가 2보다 작을 때 끝나게 됩니다.
2. 서브 리스트에도 mergeSort를 호출함으로써 반복문을 끝낼 기준이 충족할 때까지 반복됩니다. 그렇게 리스트에 element가 하나씩 존재하게 될 때 반복문은 끝납니다.
병합 함수 구현 (Merge)
이제 마지막 단계로 위 카드 정렬 예제처럼 합쳐가며 정렬해야 합니다. 이제 두 개의 리스트를 합쳐가며 정렬하는 함수를 구현해보겠습니다.
Merge
private fun <T : Comparable<T>> merge(left: List<T>, right: List<T>): List<T> {
//1
var leftIndex = 0
var rightIndex = 0
//2
val result = mutableListOf<T>()
//3
while (leftIndex < left.size && rightIndex < right.size) {
val leftElement = left[leftIndex]
val rightElement = right[rightIndex]
//4
if(leftElement < rightElement){
result.add(leftElement)
leftIndex += 1
} else if(leftElement > rightElement) {
result.add(rightElement)
rightIndex += 1
} else {
result.add(leftElement)
leftIndex += 1
result.add(rightElement)
rightIndex += 1
}
}
//5
if(leftIndex < left.size) {
result.addAll(left.subList(leftIndex, left.size))
}
if(rightIndex < right.size) {
result.addAll(right.subList(rightIndex, right.size))
}
return result
}1. 왼쪽과 오른쪽 위치를 기록합니다.
2. mutablelist에 저장합니다.
3. 리스트에 앞부분부터 왼쪽과 오른쪽을 비교합니다. 리스트에 끝에 다라면 더 이상 비교할 값이 없어집니다.
4. 두 element를 비교해서 작은 값이 result에 들어갑니다 만약 left right이 같다면, 두 개다 result에 들어가게 됩니다.
5. 첫 번째 반복문에서 오른쪽 왼쪽이 비어있지 않음을 증명했습니다. 두 리스트가 정렬되었기 때문에, 우리는 남아있는 값이 마지막 위치에 있는 result와 같거나 크다는 게 증명되기 때문에 남는 값은 비교 없이 추가해줍니다.
마무리
이제 나누고 합치는 함수들을 구현해주었습니다. 아래에서 마지막 버전의 병합 정렬을 구현해주겠습니다.
fun <T : Comparable<T>> List<T>.mergeSort(): List<T> {
if (this.size < 2) return this
val middle = this.size / 2
val left = this.subList(0, middle).mergeSort()
val right = this.subList(middle, this.size).mergeSort()
return merge(left, right)
}이제 병합 정렬을 메인 문에 구현해보겠습니다.
"merge sort" example {
val list = listOf(7, 2, 6, 3, 9)
println("Original: $list")
val result = list.mergeSort()
println("Merge sorted: $result")
}구현 결과입니다.
---Example of merge sort---
Original: [7, 2, 6, 3, 9]
Merge sorted: [2, 3, 6, 7, 9]
정리
병합 정렬의 최악 최선 평균 시나리오 속도는 O(n log n)입니다. 어떠한 상황에서도 준수한 속도를 낼 수 있다는 것에 몹시 효율적인 알고리즘입니다.
하지만 기존의 데이터를 담을 추가적인 배열 공간이 필요하다는 점에서 메모리 활용이 비효율적입니다. 나중에 배울 힙정렬은 이 메모리 비효율성 문제를 해결해줍니다.
'개발공부 > Algorithm' 카테고리의 다른 글
| [알고리즘] Heapsort 힙정렬: 필수 기본정리 - 힙정렬 원리, 구현 (0) | 2021.10.29 |
|---|---|
| [알고리즘] Radix Sort 기수 정렬 : 필수 기본정리 - 쉬운 원리 설명, 버켓 구현 - Kotlin (0) | 2021.10.26 |
| [알고리즘] O(n2) 3가지 기본 정렬 알고리즘 : 버블 정렬, 선택정렬, 삽입정렬 Kotlin 구현 (0) | 2021.10.23 |
| [알고리즘] Priority Queues 우선순위 큐: 필수 기본 정리 - 구현, 활용, comparable, comparator (0) | 2021.10.18 |
| [알고리즘] Heap 힙 데이터구조 : 필수 기본정리 - Min Heap, Max Heap, 삽입, 제거, 탐색 구현 (0) | 2021.10.18 |
![[알고리즘] Merge Sort 병합정렬 : 필수 기본 정리 - 구현, split, merge 코드 설명 - Kotlin](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FuXDpL%2FbtriGVf6KDz%2FWNbJLwzYUBxYK7QU6NX2Vk%2Fimg.png)