목차
힙 정렬은 전 포스트에서 다뤘던 버블 정렬, 선택 정렬, 삽입 정렬과 같이 비교 연산을 통해 정렬합니다. 힙을 사용하기 때문에 여러 장점이 있습니다. 바로 최솟값과 최댓값을 찾는데 최적화되어있습니다. 이 특성을 이용하여 정렬하는 것을 HeapSort라고 합니다. 이포스트를 보기 전 힙 데이터 구조를 설명한 이전 포스트를 보고 오는 것을 추천드립니다.
[알고리즘] Heap 힙 데이터구조 : 필수 기본정리 - Min Heap, Max Heap, 삽입, 제거, 탐색 구현
목차 힙(Heap) 개념 힙은 우선 우선순위의 개념을 대입한 자료구조입니다. 전포스트에서 다뤘던 Stack,Queue와 같이 자료가 들어오고 나가는 순서를 정할수있습니다. 우선순위개념과 Stack Queue에대하
underdog11.tistory.com
힙의 특성을 이용한 힙 정렬
최댓값과 최솟값을 찾는데 최적화되어있는 이유는 heap의 특성상 최대 힙일 때는 가장 큰 값이 루트 노드로 오게 되고 최소 힙일 때는 가장 작은 값이 루트 노드로 오기 때문입니다.

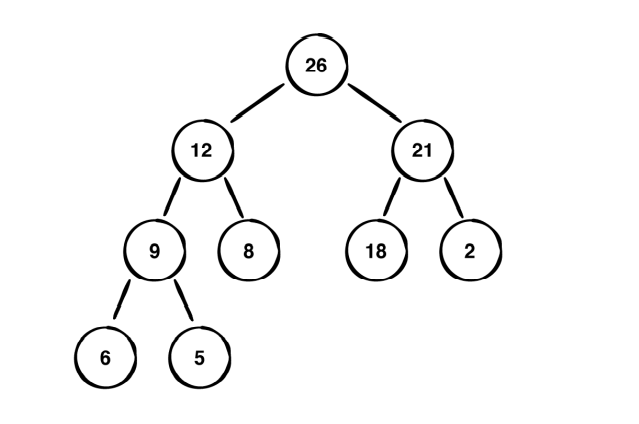
heap의 특성을 활용하기 위해 정렬되지 않은 array를 heap으로 바꿔줘야 합니다. Array를 힙으로 변환할 때 element를 heap구조에 맞는 위치에 element를 옮길 때 O(log n)의 속도를 가지고 있기 때문에, 여러 개의 element를 옮기게 되면 전체적으로 heap구조로 배열하는 속도는 O(n log n)의 속도를 가지게 됩니다. 여기서 n은 옮기게 되는 element의 수입니다.
힙 정렬 과정
정렬되는 과정을 자세히 살펴보겠습니다.
Step 1. 최대 힙의 루트 노드를 마지막 배열 값과 교환. 가장 큰 값을 마지막 배열에 저장. 그리고 가장 크고 마지막 배열에 있는 값을 힙에서 제거.

Step 2. 다시 힙을 재구조화시킴으로써 10을 제외한 최대 힙이 root자리를 다시 가져가게 됨
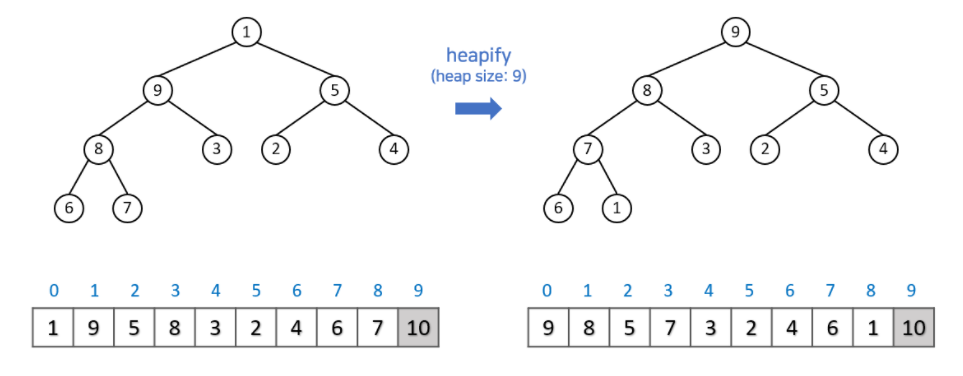
Step 3. 새로 생신 최대 힙을 배열에 10 을제 외한 마지막 배열과 교환. 즉 루트 노드인 9는 1이 있는 위치로 바뀌게 됩니다.

Step 4. 위 과정을 반복하여줍니다.
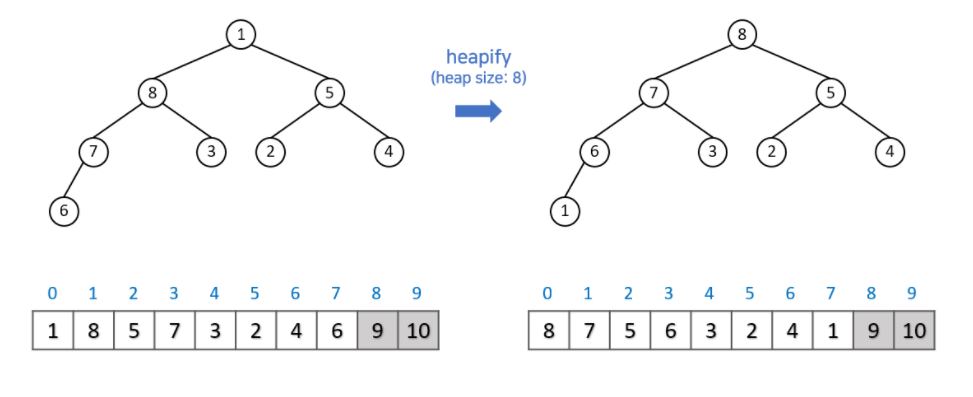
Step 5. 모두 정렬될 때까지 반복하겠습니다.

힙 정렬 코드 구현을 위한 셋업
위에서 설명했던 힙 정렬 과정대로 구현해보겠습니다.
우선 정렬은 Array에서 이루어지고, Array를 힙 구조 특성을 가지기 위해 힙 알고리즘을 불러오게 됩니다. 그리고 heapify를 이용하여, element를 정렬해야 합니다.
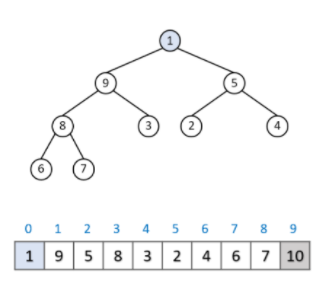
먼저 Array에서 힙처럼 정렬하기 위해서는 힙이 Array모양으로 나타나 있을 때 오른쪽 왼쪽 자식 노드의 index가 무엇인지 알아야 합니다. 아래 코드는 힙 데이터를 설명한 이전 포스트에서 다뤘습니다. 과정이 궁금하시다면 이전 포스트를 참고해주세요.
private fun leftChildIndex(index: Int) = (2 * index ) + 1
private fun rightChildIndex(index: Int) = (2 * index ) + 2ShiftDown구현
위 정렬 과정에서 봤듯이 가장 큰 값이 위로 올라가 야하기 때문에 heap포스트에서 다뤘던 shiftDown함수가 필요합니다. shift함수에 대하여 자세한 건 저번 힙 포스트에서 다뤘습니다.

저번 포스트에서 썼던 shiftDown 함수를 힙 정렬에 맞게 다시 써주도록 하겠습니다.
fun <T> Array<T>.siftDown(
index: Int,
upto: Int,
comparator: Comparator<T>
) {
var parent = index
while(true){
val left = leftChildIndex(parent)
val right = rightChildIndex(parent)
var candidate = parent
if(left < upto &&
comparator.compare(this[left], this([candiate]) > 0)
) {
candidate = left
}
if(right < upTo &&
comparator.compare(this[right], this[candidate]) > 0
) {
candidate = right
}
if (candidate ==parent) {
return
}
this.swapAt(parent, candidate)
parent = candidate
}
}힙에서 썻던 shiftdown과 정렬에서 쓰는 shiftdown함수의 다른 점은, comparator을 사용한다는 점입니다. comparator은 두 값을 비교하고, comparable은 현재 값과 다른 값을 비교한다는 점이 다릅니다.
Heapify 구현
이제 heapify 함수를 구현해줘야 합니다. heapify는 주어진 데이터를 힙 성질을 만족하도록 만드는 것을 뜻합니다. 이곳에서 element를 정렬하기 위해 만들어줬던 shiftdown함수를 사용하게 됩니다.
fun <T> Array<T>.heapify(comparator: Comparator<T>) {
if(this.isNotEmpty()) {
(this.size / 2 downTo 0).forEach{
this.siftDown(it, this.size, comparator)
}
}
}힙 정렬 구현
heapSort를 구현
마지막으로 힙 정렬을 구현해주겠습니다.
fun<T> Array<T>.heapSort(comparator: Comparator<T>) {
this.heapify(comparator)
for(index in this.indices.reversed()){ //1
this.swapAt(0,index)//2
shiftDown(0, index, comparator)//3
}
}위 코드를 자세히 알아보겠습니다.
1. 먼저 Array가 힙 형식으로 바뀌도록 재배치해줍니다.
2. array에 element를 반복하여 접근합니다.
3. 첫 번째와 마지막 element를 바꿔줌으로써 가장 큰 값이 array상으로 뒤로 가게 됩니다.

4. 위와 같이 swap후 힙 구조 규칙에서 벗어난 것을 확인할 수 있습니다. 그래서 siftdown을 통해 9 10을 제외한 가장 큰 값을 찾아 root노드에 위치시킵니다.

이제 메인 문에서 실행시켜 보겠습니다.
"Heap sort" example {
val array = arrayOf(6, 12, 2, 26, 8, 18, 21, 9, 5)
array.heapSort(ascending)
println(array.joinToString())
}위 코드를 실행하면 아래와 같은 결과가 나옵니다.
--Example of heap sort---
2, 5, 6, 8, 9, 12, 18, 21, 26
정리
메모리가 최적화되는 동시에, 힙 정렬은 최악 최선 평균 속도로 O(n log n)을 가지게 됩니다.
왜냐하면, array를 한 번씩 반복하여 접근하고, 거기서 element의 위치를 바꿔줄 때, O(log n)을 사용하게 되기 때문입니다.
힙 소트의 단점은, element가 얼마나 있냐에 따라 속도가 달라지게 됩니다.
'개발공부 > Algorithm' 카테고리의 다른 글
| [알고리즘] Graph 그래프 : 필수 기본 정리 - 가중치, 방향, 무방향 그래프, 인접리스트, 인접행렬 구현 (0) | 2021.11.02 |
|---|---|
| [알고리즘] Quick Sort 퀵정렬 : 필수 기본 정리 - 로무토 분할, 호어, 효율적인 피봇값 정하기 (0) | 2021.11.01 |
| [알고리즘] Radix Sort 기수 정렬 : 필수 기본정리 - 쉬운 원리 설명, 버켓 구현 - Kotlin (0) | 2021.10.26 |
| [알고리즘] Merge Sort 병합정렬 : 필수 기본 정리 - 구현, split, merge 코드 설명 - Kotlin (0) | 2021.10.25 |
| [알고리즘] O(n2) 3가지 기본 정렬 알고리즘 : 버블 정렬, 선택정렬, 삽입정렬 Kotlin 구현 (0) | 2021.10.23 |