[알고리즘] Binary Search Tree 이진탐색 트리 : 필수기본정리 - 탐색,삽입,삭제, 검색연산, 삭제연산 - Kotlin

목차

이진 탐색트리를 알아보기전 이진트리와 익숙하시지않으시다면 아래 포스트를 참고해주세요.

[알고리즘] Binary Tree 바이너리 트리: 기본정리 - 바이너리트리 구현, 중위순회, 전위순회, 후위순

이진 탐색 트리(BSF - Binary Search Tree)

이진 탐색 트리는 시간 복잡도에서 log(n) 오퍼레이션 이기 때문에 선형 데이터 구조보다 빠른 검색을 가능하게 하고, 데이터를 삽입하거나 지울 수 있게 해주는 데이터 구조입니다.

 

이진 탐색 트리가 만들어지는데 4가지 조건이 있습니다. 

1. 노드 왼쪽 하위트리에는 노드의 키보다 작은 키가 있는 노드만 포함됩니다.

2. 노드의 오른쪽 하위 트리에는 노드의 키보다 큰키가있는 노드만 포함됩니다. (루트 노드에 오른쪽 노드 50 < 70)

3. 왼쪽및 오른쪽 하위 트리도 각각의 이진 검색 트리여야 합니다. (2개 이상의 자식 노드를 가질 수 없습니다.)

4. 중복된 키를 허용하지 않습니다. 

 

빠른 이해를 위해 아래 그림을 참고해주세요

4가지 조건이 충족된 이진 탐색 트리입니다.

 

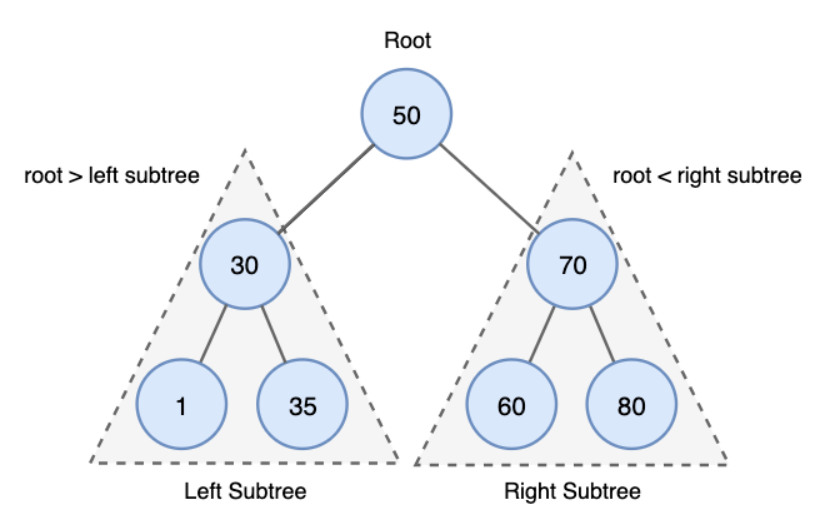
위 조건은 이진 탐색 트리가 불필요한 체크를 생략하게 하여 효율적인 검색을 가능하게 합니다. 

 

ArrayList vs 이진 탐색 트리

 

검색(Search) 비교

 

ArrayList와 이진 탐색 트리 구조를 비교해보면, 이진 탐색 트리가 훨씬 효율적인 것을 확인할 수 있습니다. 아래 예제 이미지를 통해 비교해보겠습니다. 

 

ArrayList에서 105 찾기

 

이진 탐색 트리에서 105찾기

 

ArrayList는 처음부터 105까지 도달할 때까지 하나씩 키값을 확인한 반면 이진 검색 트리에서는 105까지 3번 절차만에 도달할 것을 확인할 수 있습니다. 

 

이 이유는 이진 검색 트리의 검색 절차 특성 때문입니다.

 

위에서 다루었던, 4가지 조건을 활용하면, 탐색 값이 현재 값보다 작은 경우 왼쪽 하위 트리에 있다는 게 증명됩니다. 

만약 탐색 값보다 크다면 오른쪽 하위 트리에 있다는 게 증명됩니다. 

 

---

 

추가(Insertion) 비교

 

키값을 추가할 때도 이진 탐색 트리가 훨씬 효율적입니다. 

 

0을 추가할 때 ArrayList와 이진탐색 트리에 차이를 보겠습니다. 

 

ArrayList

ArrayList에 0을 추가할때

ArrayList에서 0을 추가할때 0이 맨 앞으로 와야 하기 때문에 공간을 만들고 1이 있던 자리에 0이 들어오고 그 뒤로 하나씩 뒤로 이동되는 걸 볼 수 있습니다. ArrayList에서 추가할 때는 시간 복잡도에서 O(n)입니다. 

 

이진 탐색 트리

 

 

이진 탐색 트리에서는 3번의 절차만에 추가할 위치를 찾아냅니다. 

 

---

 

제거(Removal) 비교

 

25를 제거하는 예제를 살펴보겠습니다. 

 

ArrayList

ArrayList에서 25 제거

ArrayList에서 25를 제거할 때, 제거한 후 40부터 하나씩 위치가 당겨짐으로써 총 6번을 반복한 것을 볼 수 있습니다. 

 

이진 탐색 트리

위와 같이 이진 탐색 트리에서는 지울 값을 효율적으로 찾아낸 걸 확인하실수 있습니다. 

 

이렇게 3가지 상황: 검색, 추가, 제거 기능에서 모두 이진 탐색 트리가 Arraylist보다 뛰어난 걸 확인할 수 있습니다.  이제 이진 검색 트리를 구현해보겠습니다. 

 

 

이진 탐색 트리 구현

 

먼저 이진탐색트리 클래스를 생성해주겠습니다. 

 

이진탐색트리 클래스

class BinarySearchTree<T: Comparable<T>>() {
	var root: BinaryNode<T>? = null
    
    override fun toString() = root?.toString() ?: "empty tree"
}

 

아래는 이진 검색 트리를 생성하기 위해 노드를 추가할 때 쓸 insert함수입니다.  

 

Insert 함수 구현

fun insert(value: T) {
	root = insert(root, value)
}

private fun insert(
	node: BinaryNode<T>?
    value: T
): BinaryNode<T> {
	//1
    node?: return BinaryNode(value)
    //2
    if(value < node.value) {
    	node.leftChild = insert(node.leftChild, value)
    } else{
    	node.rightChild = insert(node.rightChild, value)
    }
    //3 
    return node
}

위에 레이블 된 번호 순서대로 코드를 코멘트해보겠습니다: 

1. 반복문입니다. 그래서 이 반복문을 끝내는 조건이 필요합니다. 현재 노드가 null일 때, 새로 이진 노드를 넣을 자리를 찾은 것입니다. 그러면 여기에 새로운 이진 노드를 넣어줍니다. 

2. 새로운 값이, 현재 값보다 작다면, leftChild에 넣어줍니다. 만약 새로운 값이 현재 값보다 크거나 같다면, rightChild에 넣어줍니다. 

3. 다시 현재 노드로 돌아옵니다. null이 라면 node를 생성하고, null이 아니라면 node를 리턴

 

insert 함수를 활용하여 이진 탐색 트리를 만들어보겠습니다. 

 

Insert함수 사용

"building a BST" example {
val bst = BinarySearchTree<Int>()
    (0..4).forEach{
    	bst.insert(it)
    }
    println(bst)
}

위 코드를 실행하면 아래와 같습니다. 

---Example of building a BST---
   ┌──4
  ┌──3
  │ └──null
 ┌──2
 │ └──null
┌──1
│ └──null
0
└──null

**하지만 트리의 모양이 균형 잡힌 모양이 아닌, 한쪽으로 치우쳐진 모양인 것을 볼 수 있습니다. 근데 트리 특성상 균형 잡힌 트리이어야 합니다.**

 

왜냐하면 아래와 같이, 실행 속도에도 영향이 주기 때문입니다. 

위와 같이 균형 잡히지 않은(unbalanced) 형태의 트리는 4까지 도달하는데 4 스텝이 필요한 반면 balance일 때는 한 번에 도달하게 됩니다. 

val exampleTree = BinarySearchTree<Int>().apply{
	insert(3)
    insert(1)
    insert(4)
    insert(0)
    insert(2)
    insert(5)
}

트리를 보면 균형 잡힌 트리가 생성된 것을 볼 수 있습니다. 

"building a BST" example{
	println(exampleTree)
} 

---Example of building a BST---
 ┌──5
┌──4
│ └──null
3
│ ┌──2
└──1
 └──0

 

이진 탐색 트리 활용

위에서 이진 탐색 트리와 arraylist를 비교하여, 이진 검색이 검색 추가 제거 기능 면에서 모두 뛰어난 걸 확인하였습니다. 이번에는 직접 코드를 통해 이진 검색 트리에서 검색과 제거를 해보겠습니다. 

검색 연산 개념 및 구현

이진 탐색 트리에서 node를 찾는 방법은 순회를 이용하는 방법입니다. 위에서 했던, 순회 알고리즘을 사용하여 쉽게 원하는 node를 찾는 함수를 구현할 수 있습니다. 

 

contain 함수 구현

fun contain(value: T): Booleanb {
	root?: return false
	
    var found = false
    root?.traverseInOrder {
    	if(value ==it){
        	found = true
        }
    }
    return found
}

값이 있다면 true 값이 없다면 false를 리턴합니다. 

 

메인 문에 이 함수를 이용하여, tree에서 5를 찾아보겠습니다. 

 

검색연산 사용

"finding a node" example{
	if(exampleTree.contains(5)){
    	println("Found 5!")
    } else {
    	println("Couldn't find 5")
    }
}

---Example of finding a node---
Found 5!

함수를 찾는 것은 시간 복잡도에서 O(n)입니다. 즉 n 사이즈가 커질수록 오래 걸리게 됩니다. 

 

하지만 효율적으로 코드를 수정하는 법이 있습니다. 

 

효율적인 contain 함수 구현

fun contains(value: T): Boolean {
	//1
    var current = root
    
    //2
    while(current != null){
    	//3
        if(current.value == value){
        	return true
        }
        //4
        current = if(value < current.value){
        	current.leftChild
        } else{
        	current.rightChild
        }
    }
    return false
    
}

1. root노드를 현재 노드로 지정해줍니다. 

2. 현재 노드가 null이 아니라면, 현재 값을 확인합니다. 

3. 만약 현재 값이, 찾으려는 값과 같다면, true를 반환합니다. 

4. 위에 조건에 모두 해당하지 않는다면, 오른쪽이나 왼쪽 자식 노드를 확인합니다 

 

함수를 효율적으로 바꿔준후 시간 복잡도 O(n)에서 O(log n) 오퍼레이션이 되었습니다. . 

 

삭제 연산 개념

이진 탐색 트리에서 node 지우기는 까다롭습니다. 왜냐하면 지울 때 고려해야 할 3가지 상황 때문입니다. 

1. 삭제할 노드가 (1) 단말 노드인 경우

2. 삭제할 노드가 (2) 하나의 서브 트리만 가지고 있는 경우

3. 삭제할 노드가 (3) 두 개의 서브 트리를 가지고 있는 경우

 

---

 

삭제할 노드가 (1) 단말 노드인 경우

마지막 자식 노드이기 부모 노드와 연결을 끊으면 됩니다. 

---

 

삭제할 노드가 (2) 하나의 서브 트리만 가지고 있는 경우

자식을 가진 노드라면 노드를 지운 후 그 자식을 부모 노드와 연결해줍니다. 

 

---

 

삭제할 노드가 (3)두 개의 서브 트리를 가지고 있는 경우

두 개의 서브 트리를 가지고 있을 때 좀 더 복잡합니다. 위에서 했던 방식대로 더 이상 쓸 수 없습니다. 예시 그림을 보고, 설명해보겠습니다. 

25를 제거 / 위에서 했던 방식으로 지웠을때

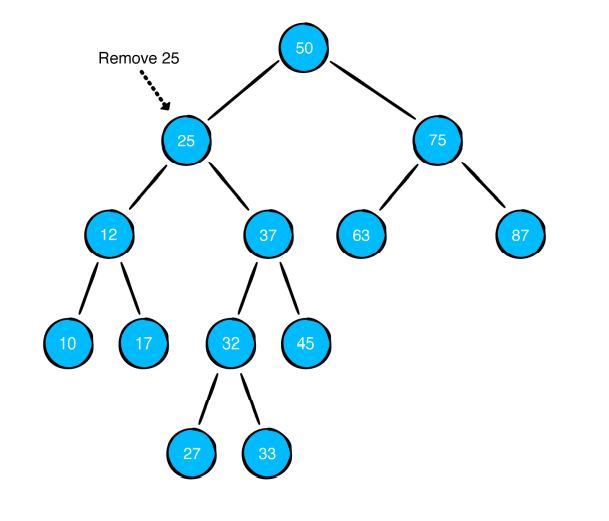
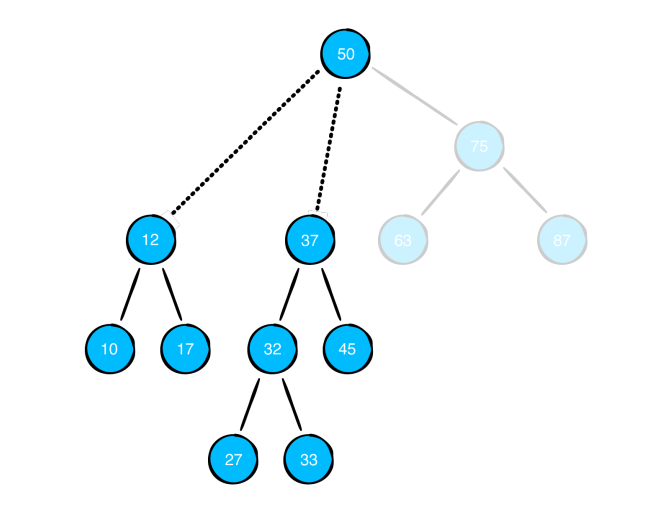
위처럼 25를 지우겠다고 가정해봅시다. 25를 지우게 되면, 루트 노드인 50은 3개의 가지를 가지게 되는데 그러면 더 이상 이진 탐색 트리라고 정의할 수 없게 됩니다. 

 

그래서 이경우에는 오른쪽 자식 중 가장 작은 값을 제거될 자리로 옮깁니다. 그래서 25 있던 자리에 27이 오게 됩니다. 

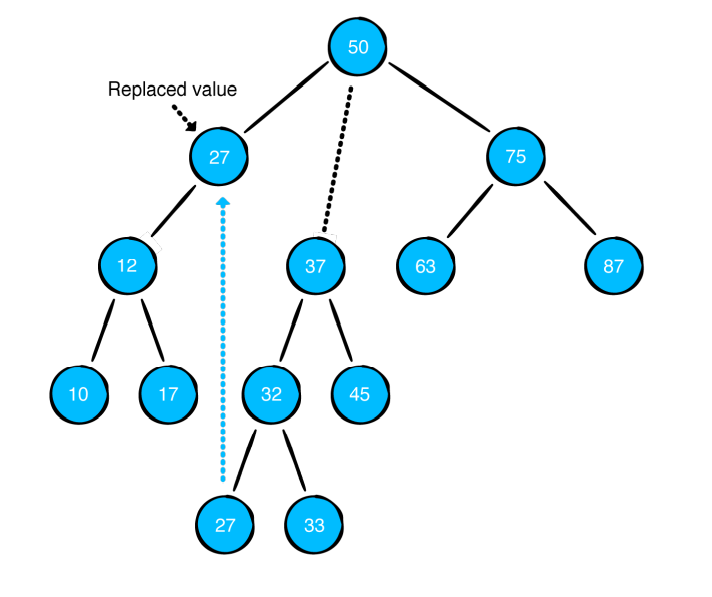
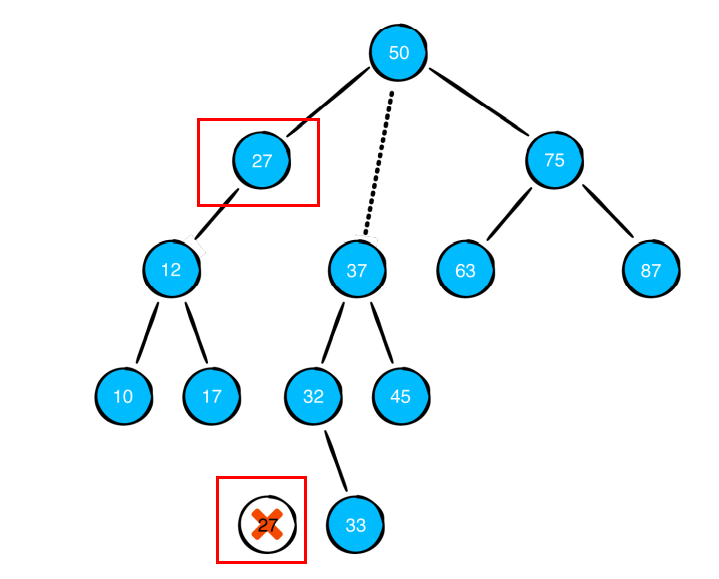
**혹은 위와 같은 방식으로 왼쪽 자식 중에서 가장 큰 값을 제거될 자리로 옮기면 됩니다.**

 

삭제 연산 구현

이진 노드를 먼저 생성해주겠습니다.

val main: BinaryNode<T>?
	get() = leftChild?.min ?: this

Binary Search Tree 이진탐색트리 클래스 아래에 remove함수를 구현해주겠습니다. 

 

Remove함수 구현

fun remove(value:T){
	root = remove(root, value)
}
private fun remove(
	node:BinaryNode<T>?,
    value:T
): BinaryNode<T>? {
	node ?: return null
    
    when{
    	value == node.value ->{
        	//1
            if (node.leftChild == null && node.rightChild == null) {
            	return null
            }
            //2
            if(node.leftChild == null){
            	returnnode.rightChild
            }
            //3
            if(node.rightChild == null){
            	return node.leftChild
            }
            //4
            node.rightChild?.min?.value?.let{
            	node.value = it
            }
            node.rightChild = remove(node.rightChild, node.value)
      
        }
        value < node.value -> node.leftChild = 
        remove(node.leftChild,value)
        else-> node.rightChild = remove(node.rightChild, value)
    }
    return node
}

1. 노드가 단말 노드일때, null을 리턴하고, 현재 노드를 제거합니다. 

2. 노드가 왼쪽자식이 없을때 노드를 리턴합니다. 그리고 오른쪽 자식을 오른쪽, 서브트리에 연결합니다.

3. 노드가 오른쪽 자식이 없을때 노드를 리턴합니다. 그리고 왼쪽 사식을 왼쪽 서브트리에 연결합니다. 

4. 노드가 오른쪽 왼쪽 자식 둘다 있을때입니다. 오른쪽 자식중 가장 작은 값과 위치를 바꿉니다. 

 

이제 이 코드를 사용해서 트리에서 3을 제거해보겠습니다. 

 

노드 제거함수 실행

"removing a node" example{
	println("Tree before removal:")
    println(exampleTree)
    exampleTree.remove(3)
    println("Tree after removing root:")
    println(exampleTree)
}

결과값은 아래와 같습니다. 

---Example of removing a node---
Tree before removal:
 ┌──5
┌──4
│ └──null
3
│ ┌──2
└──1
 └──0
Tree after removing root:
┌──5
4
│ ┌──2
└──1
 └──0

정리

- 이진 탐색 트리는 정돈된 데이터를 가지고있는 데이터 구조입니다.

- 이진 탐색 트리의 탐색,삽입, 삭제 프로세스의 평균 런타임은 시간복잡도에서 O(n)보다 빠른 O(log n) 입니다.

- 하지만 트리가 불균형한 상태라면, O(log n)에서 O(n)으로 느려집니다.