[알고리즘] Binary Tree 이진 트리: 기본정리 - in-order 중위순회, pre-order 전위순회, post-order 후위순회 구현 - Kotlin

목차

이번 포스트에서는 이진 트리에 대해서 알아보겠습니다. 이진 트리를 알아보기전, 트리의 용어와 익숙하시지않으시다면 아래 포스트를 먼저 보고와주세요. 

[알고리즘] Tree 트리 : 기본정리 - 트리 구성, 깊이우선순회(Depth-First Traversal), 레벨순회(LevelOrderTra

이진 트리 개념

이진 트리는 트리와 같지만 최대 2개의 자식만 가질 수 있는 트리구조입니다. 

 

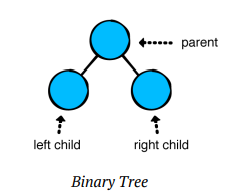
자식 두 개의 왼쪽을 LeftChild 오른쪽을 rightChild로 부릅니다. 

 

이진 트리 구현하기

이진 트리를 구성하기 앞서, 이진트리에 노드 클래스를 만들어줘야 합니다. 노드를 생성해줬으니, 이진트리를 만들 수 있게 되었습니다. 

typealias Visitor<T> = (T)-> Unit

class BinaryNode<T>(val value : T) {

	var leftChild: BinaryNode<T>? = null
    var rightChild: BinaryNode<T>? = null
    
}

메인 문에서 이진 노드를 활용하여이진 트리를 구현해보겠습니다. 

fun main() {
	val zero = BinaryNode(0)
    val one = BinaryNode(1)
    val five = BinaryNode(5)
    val seven = BinaryNode(7)
    val eight = BinaryNode(8)
    val nine = BinaryNode(9)
    
    seven.leftchild = one
    one.leftChild = zero
    one.rightChild = five 
    seven.rightChild = nine
    nine.leftChild = eight
    
    val tree = seven
}

위 코드를 실행하면 아래와 같은 이진트리가 만들어집니다. 

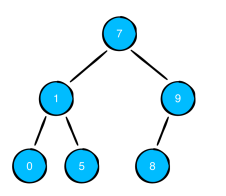
코드로 트리 다이어그램 만들기(선택)

이진 트리를 만들고 나서 어떻게 트리가 만들어지는지 보기 위해 트리를 그려보면 이해하는데 도움이 됩니다. 하지만 트리 크기가 커지면 손으로 그리기 오래 걸리기 때문에 아래 코드를 사용하여 코드가 다이어그램을 만들도록 할 수 있습니다. 

 

아래 함수는 Karoly Lorentey - Optimizing Collection 책을 참조하였습니다. 

Optimizing Collections

이진트리 다이어그램을 만들어주는 코드입니다. 

override fun to String() = diagram(this)

private fun diagram(node: BinaryNode<T>?, 
					top: String = "",
                    root: String = "",
                	bottom: String = ""): String {
	return node?.let{
    		if (node.leftChild = null && node.rightChild == null) {
        	"$root${node.value}\n"
        	} else {
        	diagram(node.rightChild, "$top ", "$top┌──", "$top│ ") +
 			root + "${node.value}\n" + diagram(node.leftChild, 
			"$bottom│ ", "$bottom└──", "$bottom ")
 		}
 	} ?: "${root}null\n"
}

위 코드를 붙여 넣기 하여 실행해 봅시다. 

println(tree)

실행하면 아래와 같은 코드가 나옵니다. 

   ┌──null
┌──9
│ └──8
7
│  ┌──5
└──1
  └──0

이진 트리를 이용한 순회 구현

 

트리에서 했던것처럼 이진 트리도 순회 알고리즘을 구현할 수 있습니다. 트리에 대하여 자세히 알고 싶으시다면 아래 포스트를 참조해주세요.

[알고리즘] Kotlin Tree 기본정리 개념,구성, 알고리즘 쉬운 예제 - 깊이우선순회( Depth-First Traversal),

이진트리에서는 아래 3가지 순회가 존재합니다.

 

1. 중위 순회(In-order)

2. 전위 순회(pre-order)

3. 후위 순회(post-order)

 

중위 순회(In-order) 

중위 순회의 특징은 아래와 같은 순서로 이동한다는 점입니다.

left -> root -> right

왼쪽자식노드 -> 부모노드-> 오른쪽 자식 노드

왼쪽 자식 노드 먼저 시작하기 때문에, 가장 깊이가 깊은 자식 노드인 8번 왼쪽 자식 노드부터 시작하게 됩니다. 

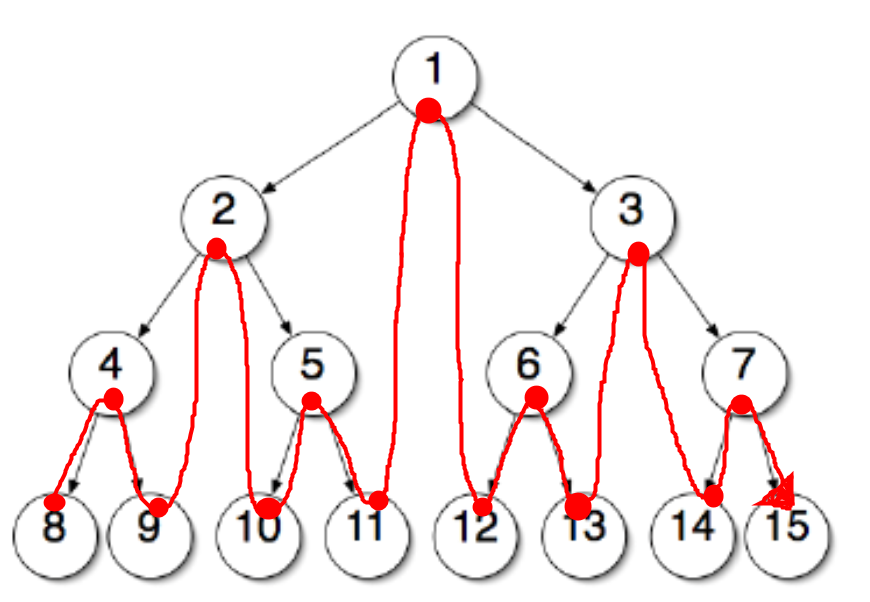
중위 순회로 실행하면 8 > [4] > 9 > [2] > 10 > [5] > 11 > [1] > 12  > [6] > 13 > [3] > 14 > [7] > 15

 

코드로 중위순회 함수를 구현해보겠습니다. 아래 함수를 추가해주시면 됩니다. 

fun traverseInOrder(visit: Visitor<T>) {
	leftChild?.traverseInOrder(visit)
    	visit(value)
        rightChild?.traverseInOrder(visit)
}

코드를 실행해보겠습니다. 

tree.traverseInOrder { println(it)}

트리는 위에서 만들어줬던 Binary Tree를 사용해보겠습니다. 

0
1
5
7
8
9

 

전위 순회(pre-order)

전위 순회 알고리즘은 아래와 같은 순서로 접근합니다. 

root -> left -> right 
부모노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드

 

아래 이진트리를 전위 순회로 접근했을 때 순서를 보겠습니다. 

 

 

전위 순회로 실행하면  [1] > [2] > [4] > 8 > 9 > [5] > 10 > 11 > [3] > [6] > 12 > 13 > [7] > 14 > 15

 

전위 함수를 코드를 구현하면 아래와 같습니다.

fun traversePreOrder(visit: Visitor<T>) {
	visit(value)
    	leftChild?.traversePreOrder(visit)
    	rightChild?.traversePreOrder(visit)
}

전위 순회 함수를 실행해보겠습니다. 

tree.traversePreOrder { println(it) }

사용했던 트리를 사용하여 전위 순회 함수를 실행하면 다음과 같은 결과가 나옵니다. 

7
1
0
5
9
8

 

후위 순회(post-order)

후위 순회의 순서는 아래와 같습니다.

left -> right -> root
왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 부모 노드

화살표를 따라가보세요.

 

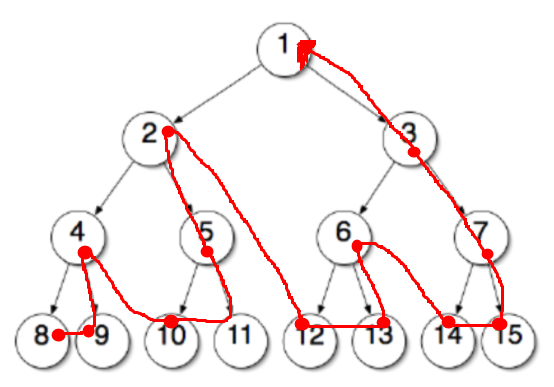
후위 순회로 실행하면 8 > 9 > [4] >10 >11 > [5] > [2] > 12 > 13 > [6] > 14 > 15 > [7] > [3] > [1]

 

코드로 구현해보겠습니다. 

fun traversePostOrder(visit: Visitor<T>) {
	leftCHild?.traversePostOrder(visit)
    	rightChild?.traversePostOrder(visit)
    	visit(value)
}

 

위 코드를 실행해보겠습니다. 

tree.traversePostOrder { println(it) }

0
5
1
8
9
7

다음 포스트에서는 이진 탐색트리를 알아보도록 하겠습니다. 

[알고리즘] Binary Search Tree 이진탐색 트리 : 필수기본정리 - 탐색,삽입,삭제, 검색연산, 삭제연산 -