[알고리즘] Tree 트리 : 기본정리 - 트리 구성, 깊이우선순회(Depth-First Traversal), 레벨순회(LevelOrderTraversal), 검색(Search) - Kotlin

목차

Tree 개념

 

Tree는 데이터 구조중 하나입니다.

1. 계층구조의 관계를 가진 데이터 구조이고

2. 정리되어 나열된 데이터를 다룰 때 검색이 빠릅니다.

3. Tree에는 사이즈, 모양이 다른 여러 tree들 이 있습니다.

4. 트리는 노드들과 노드들을 연결하는 링크로 구성되어있습니다.

 

 

Tree 구성 및 용어

 

우선 시작하기에 앞서 tree에 구성과 용어들을 살펴보겠습니다.

 

용어	설명	다이어그램
Node	LinkedList와 비슷하게 tree에도 node가 있습니다. 각 node는 데이터를 포함하고있습니다.
Parent(부모) / Child(자식)	부모노드는 다수의 자식 노드를 가지고있을수있습니다. 하지만 자식 노드는 하나의 부모만 가지고있을수있습니다.
루트 노드(Root)	트리에 가장 상단에 위치한 노트입니다. 부모가 없고 트리는 하나의 루트 노드만을 가집니다.
단말 노드(Leaf)	자식이없는 노드입니다. 트리에 가장 끝부분에 위치합니다.
노드의 크기(Size)	자신을 포함한 자식 노드의 수	Size = 6
노드의 깊이(Depth)	루트에서 특정노드 까지 도달하는데 거쳐야하는 간선의 수	B의 깊이 2 D의 깊이 3
노드의 레벨(Level)	트리에 특정 깊이를 가진 노드의 집합	A의 레벨 1 B와 C의 레벨 2 D E F 레벨 3
노드의 차수(Degree)	각 노드가 가진 가지의 수	B의 차수: 3 A의 차수 2
트리의 차수	트리의 최대 차수	B가 가장 많은 가지수를 가지고있기때문에 트리의 차수는 3
트리의 높이	루트 높이에서 가장 깊이있는 노드의 깊이	트리의 높이3

 

Tree 구현하기

 

Tree는 node들로 구성되어있습니다. 먼저 TreeNode클래스를 만들어주겠습니다.

class TreeNode<T>(val value: T) {
	private val children:MutableList<TreeNode<T>> =
    mutableListOf()
}

각 노드는 노드 안에 값과 자식 노드 정보들을 mutableList에 저장합니다.

 

Add 함수 추가

 

Add함수는 자식 노드를 노드에 추가하는 함수입니다.

fun add(child: TreeNode<T>) = children.add(child)

지금 만들어진 클래스와 Add함수로 트리를 main문에 만들어보겠습니다.

fun main() {
	val hot = TreeNode("Hot")
    val cold = TreeNode("Cold")
    
    val beverages = TreeNode("Beverages").run {
    	add(hot)
        add(cold)
    }
}

위 코드를 그림으로 나타내면 아래와 같습니다.

 

트리 순회 알고리즘(Traversal Algorithem)

리스트의 순회

리스트에서 반복은 시작과 끝이 정해져 있어서 쉬웠지만 트리는 여러 개의 끝이 있기 때문에, 더 복잡합니다. 하나하나 모두 접근하기 위해 여러 전략이 있습니다. 가장 먼저 깊이 우선 탐색(Depth First Traversal)입니다. 

 

트리의 순회

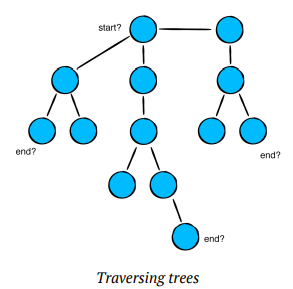
깊이 우선 순회 (Depth-First-Traversal)

루트 노드나 임의의 노드에서 시작하여 최대로 진입할 수 있는 깊이까지 탐색하고 다시 돌아와 다른 노드로 같은 방식으로 탐색을 하는 방식입니다.

• 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사합니다.
• 즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것입니다.
• 사용하는 경우: 모든 노드를 방문하고자 하는 경우에 이 방법을 선택합니다.

---

forEachDepthFirst 함수 구현

fun forEachDepthFirst(visit: Visitor<T>) {
	visit(this)
    children.forEach{
    	it.forEachDepthFirst(visit)
    }
}

깊이 우선 순회를 활용해 예제를 다뤄보겠습니다.

 

---

 

Tree 생성

 

먼저 Tree를 만들어주겠습니다.

fun makeBeverageTree(): TreeNode<String> {
 	val tree = TreeNode("Beverages")
 	val hot = TreeNode("hot")
 	val cold = TreeNode("cold")
 	val tea = TreeNode("tea")
 	val coffee = TreeNode("coffee")
 	val chocolate = TreeNode("cocoa")
 	val blackTea = TreeNode("black")
 	val greenTea = TreeNode("green")
 	val chaiTea = TreeNode("chai")
 	val soda = TreeNode("soda")
 	val milk = TreeNode("milk")
 	val gingerAle = TreeNode("ginger ale")
 	val bitterLemon = TreeNode("bitter lemon")
 	
	tree.add(hot)
 	tree.add(cold)
 	
    hot.add(tea)
 	hot.add(coffee)
 	hot.add(chocolate)
  	
    cold.add(soda)
 	cold.add(milk)

	tea.add(blackTea)
 	tea.add(greenTea)
 	tea.add(chaiTea)
 	
    soda.add(gingerAle)
 	soda.add(bitterLemon)
 return tree
}

위 코드를 트리 다이어그램으로 보면 아래와 같습니다.

---

 

활용 예제

 

Tree가 준비되었기 때문에, 깊이 우선 순회 함수로 각 node에 접근해보겠습니다. 

 

fun main() {
	val tree = makeBeverageTree()
	tree.forEachDepthFirst { println(it.value) }
}

main문을 실행하면 다음과 같습니다:

Beverages
hot
tea
black
green
chai
coffee
cocoa
cold
soda
ginger ale
bitter lemon
milk

프린트된 항목들은 이렇게 가장 깊이 있는 항목들을 접근 후 끝에 도달하면 가자 갈림길로 돌아가서 또다시 가장 깊은 곳까지 접근을 시도하는 것을 볼 수 있습니다. 그리고 tea자식들에서 가장 깊은곳까지 접근후 coffee와 cocoa 접근후 가장 상단으로 돌아가 hot과 cold의 갈림길로 들어갑니다. 그리고 cold로 이동해주는것을 알수있습니다. 

레벨 순회 (Level Order Traversal)

Node에 레벨을 기준으로 접근합니다. Root에서 시작해서 아래 레벨로 이동하기위해서 현재레벨을 모두 접근해야 아래레벨로 이동 가능합니다.

fun forEachLevelOrder(visit: Visotor<T>) {
	visit(this)
    val queue = Queue<TreeNode<T>>()
    children.forEach { queue.enqueue(it) }
    
    var node = queue.dequeue()
    while(node != null){
    	visit(node)
        node.children.forEach{ queue.enqueue(it) }
        node = queue.dequeue()
    }
}

위에서부터 아래로, 왼쪽에서 오른쪽 순서로 이동합니다.

레벨 순회의 특징은 큐를 활용하여 순회한다는 점입니다. 순회 과정입니다.

1. 큐 생성 및 초기화

2. 큐에 루트 노드 삽입 (Enqueue a 삽입)

3. 큐가 empty가 될 때까지 반복 (반복문 시작 -> Dequeue진행)

4. Dequeue연산을 통해 노드(N)를 추출 (처음에는 Root node a)

5. 위에서 추출된 N을 방문

6. N의 왼쪽 자식이 있다면 그 자식을 큐에 삽입 (Enqueue)

7. N의 오른쪽 자식이 있다면 그 자식을 큐에 삽입 (Enqueue)

 

활용 예제

 

main문에 실행해보겠습니다.

fun main(){
	val tree = makeBeverageTree()
    tree.forEachLevelOrder { println(it.value) }
}

메인 문을 실행한 결과입니다.

beverages
hot
cold
tea
coffee
cocoa
soda
milk
black
green
chai
ginger ale
bitter lemon

1 레벨을 접근하면 자식 노드인 2 레벨을 접근

dequeue를 해서 2 레벨에 있는 노드들을 추출

추출한 값에서 왼쪽에 있는 node먼저 child값을 queue에 추가

dequeue를 해서 3 레벨(왼쪽)에 있는 노드들을 추출

이제 2 레벨 오른쪽에 있는 node child값을 추가

dequeue 해서 3 레벨(오른쪽)에 있는 노드들을 추출(자식이 없으면 다음 오른쪽 노드로 넘어감)

...

level 4까지 반복

 

 

Search 탐색 함수

위에서 하나씩 데이터에 접근해보는 함수들을 만들었기때문에, search를 만드는 것은 쉽습니다. 위 함수중 forEachLevelOrder을 사용해서 탐색 함수를 만들어보겠습니다. 

 

fun search(value: T): TreeNode<T>? {
	var result: TreeNode<T>? = null
    
    forEachLevelOrder {
    	if (it.value == value){
        	result = it
        }
    }
    return result
}

 

value가 우리가 찾는 값이고 forEachLevelOrder에서 조건이 충족될때, result값을 it으로 지정하고 result를 리턴합니다. main문에서 실행해보겠습니다.

 

fun main() {
	val tree = makeBeverageTree()
    tree.search("ginger ale")?.let{
    	println("found node: ${it.value}")
    }
    tree.search("WKD Blue")?.let {
    	println(it.value)
    } ?: println("Couldn't find WKD Blue")
}

 

결과는 다음과 같습니다. 

Fouond node: ginger ale
Couldn't find WKD Blue

 

다음 포스트에서는 이진 트리를 알아보도록 하겠습니다. 

[알고리즘] Binary Tree 바이너리 트리: 기본정리 - 바이너리트리 구현, 중위순회, 전위순회, 후위순